자료: http://en.wikipedia.org/wiki/Geometric_series
(...) The sum of a geometric series is finite as long as the terms approach zero; as the numbers near zero, they become insignificantly small, allowing a sum to be calculated despite the series being infinite. The sum can be computed using the self-similarity of the series.
[edit]Example
Consider the sum of the following geometric series:
This series has common ratio 2/3. If we multiply through by this common ratio, then the initial 1 becomes a 2/3, the 2/3 becomes a 4/9, and so on:
This new series is the same as the original, except that the first term is missing. Subtracting the new series (2/3)s from the original series cancels every term in the original but the first:
A similar technique can be used to evaluate any self-similar expression.
[edit]Formula
For  , the sum of the first n terms of a geometric series is:
, the sum of the first n terms of a geometric series is:
 , the sum of the first n terms of a geometric series is:
, the sum of the first n terms of a geometric series is:where a is the first term of the series, and r is the common ratio. We can derive this formula as follows:
The formula follows by multiplying through by a.
As n goes to infinity, the absolute value of r must be less than one for the series to converge. The sum then becomes
When a = 1, this simplifies to:
the left-hand side being a geometric series with common ratio r. We can derive this formula:
The general formula follows if we multiply through by a.
This formula is only valid for convergent series (i.e., when the magnitude of r is less than one). For example, the sum is undefined when r = 10, even though the formula gives s = −1/9.
This reasoning is also valid, with the same restrictions, for the complex case.
(...)
Economics
Main article: Time value of money
In economics, geometric series are used to represent the present value of an annuity (a sum of money to be paid in regular intervals).
For example, suppose that you expect to receive a payment of $100 once per year (at the end of the year) in perpetuity. Receiving $100 a year from now is worth less to you than an immediate $100, because you cannot invest the money until you receive it. In particular, the present value of a $100 one year in the future is $100 / (1 + I), where I is the yearly interest rate.
Similarly, a payment of $100 two years in the future has a present value of $100 / (1 + I)2 (squared because it would have received the yearly interest twice). Therefore, the present value of receiving $100 per year in perpetuity
can be expressed as an infinite series:
This is a geometric series with common ratio 1 / (1 + I). The sum is
For example, if the yearly interest rate is 10% (I = 0.10), then the entire annuity has a present value of $1000.
This sort of calculation is used to compute the APR of a loan (such as a mortgage loan). It can also be used to estimate the present value of expected stock dividends, or the terminal value of a security.
(...)



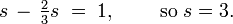

![\begin{align}
&\text{Let }s = a + ar + ar^2 + ar^3 + \cdots + ar^{n-1}. \\[4pt]
&\text{Then }rs = ar + ar^2 + ar^3 + ar^4 + \cdots + ar^{n} \\[4pt]
&\text{Then }s - rs = s(1-r) = a-ar^{n},\text{ so }s = a \frac{1-r^{n}}{1-r}.
\end{align}](http://upload.wikimedia.org/wikipedia/en/math/a/b/4/ab40c376fc277aea250484fa64b8701c.png)

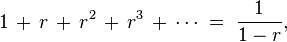
![\begin{align}
&\text{Let }s = 1 + r + r^2 + r^3 + \cdots. \\[4pt]
&\text{Then }rs = r + r^2 + r^3 + \cdots. \\[4pt]
&\text{Then }s - rs = 1,\text{ so }s(1 - r) = 1,\text{ and thus }s = \frac{1}{1-r}.
\end{align}](http://upload.wikimedia.org/wikipedia/en/math/c/a/e/caed3679cb96a5b26a3fcb30f2518e6d.png)







댓글 없음:
댓글 쓰기