자료: SSRN
By Eric Tymoigne, Lewis & Clark College
Levy Economics Institute Working Paper No. 483 , December 2006
※ Thanks to the author and the SSRN for providing the article on the Internet. This reader wants to study the content with some annotations and underlines, so anyone who is interested in it is kindly invited to visit the source link at the top.
※ Keywords: Real Interest Rate, Fisher
※ 검색어: Fisher, marginal rate of return over cost
※ Keywords: Real Interest Rate, Fisher
※ 검색어: Fisher, marginal rate of return over cost
Abstract:
By providing five different criticisms of the notion of real rate, the paper argues that this concept, as Fisher defined it or as a definition, is not relevant to economic analysis. Following Keynes and other post-Keynesians, the article shows that the notion of real rate is microeconomically and macroeconomically unfounded. Adjusting interest rates for inflation does not protect the purchasing power of wealth, and it is impossible to do so at the macroeconomic level. In addition, an empirical interpretation of the break in the correlation between interest rates and inflation since 1953 is provided.
Fisher’s real rate of interest framework is essential for the inflation-targeting framework. It provides a rationale for the idea that monetary policy should be concerned mainly (if not only) with managing inflation expectations in order to keep real interest rates at a stable level that promotes saving and investment. Some post-Keynesians, like Smithin (2003) or Cottrell (1994), have also promoted the use of this concept, even if the former claimed that it only represents a definition and does not have anything to do with Fisher. Many authors have challenged the notion of real rate at the empirical level but only a few have done it at the theoretical level. Among those exceptions are authors like Keynes, Hahn, Harrod, Davidson, and Kregel.
The present article continues such critique and argues that the notion of real rate is not theoretically relevant for the study of micro- or macroeconomic problems—it does not protect against potential losses of purchasing power and the underlying arbitrage is impossible to do at the macroeconomic level. The paper also contributes to the large empirical literature on the subject by providing an interpretation of the break that occurred in the mid 1960s in the correlation between interest rates and inflation. In the end, we conclude that economic agents are far more concerned with nominal matters (i.e., financial power, or liquidity and solvency) than real problems (purchasing power). Not that the latter is ignored or unimportant, but it included into the broader considerations of the former.
The first four parts of the paper provide a theoretical criticism of Fisher’s theory, the fifth part of the paper provides an empirical study of the Fisher’s effect, and the paper concludes with an explanation of the relevance of nominal values.
1. ANTICIPATED INFLATION DOES NOT AFFECT NOMINAL INTEREST RATE
The first criticism of Fisher’s theory was provided by Keynes in the General Theory (1936). This criticism was restated and developed by Harrod (1971) and Davidson (1974, 1986). We know that, for Fisher, at the aggregate level:
i = r* + E(π)Thus, given r* (the required real rate determined independently in the loanable funds market), any expected increase (decrease) in the rate of inflation will lead to an increase (decrease) in the nominal rate of interest via arbitrages between future and present aggregate incomes. Indeed, say that in time t = 0, the economy is at a full employment equilibrium with no inflation expected (i_0 = r*). Suddenly, in time t = 1, the central bank is expected to increase the money supply in time 2 so that, following the quantity theory of money, there is some inflation expected: E_1(π_2) = m_2 so that, in time 1, i_0 – E_1(π_2) < r*. Aggregate real income grows at a faster rate than the expected real amount of money that needs to be reimbursed (and so, too, the expected amount of real aggregate income to give up in the future if one borrows). The willingness to smooth consumption gives an incentive to borrow money now in order to buy some present income while giving up some future income. This puts an upward pressure on the money-rate on money:
If inflation is going on, he will see rising prices and rising profits, and will be stimulated to borrow capital unless interest rate rises; moreover, this willingness to borrow will itself raise interest rate. (Fisher 1907)Theoretically, i should grow immediately to compensate for E_1(π_2) and no real effect should occur from the rise of money because the required and expected real rates are equal: i_1 – E_1(π_2) = r*, with i_1 > i_0.[주1]
[주1] Inflation will occur because of the increase in the money supply by the central bank.
Keynes was the first to have some difficulties with this explanation of the business cycle. His direct criticism rests on three points, with the third one being the consequences of the first two.
- First, what should be compared are the money-rates, not the real rates, because the former are the only observable and the liquidity of position is essential—capital gain/loss should be included in the yield rate calculation.[주2]
- Second, capital assets are usually not a good substitute for monetary assets as a store of value, whereas there is a high substitutability among monetary assets, and between monetary assets and liquid non-monetary assets.
- Third, for the two preceding reasons, Fisher’s explanation of what drives the interest rate on money is invalid. Changes in interest rates do not reflect changes in the opportunity cost induced by inflation in the present/future consumption arbitrage, they reflect changes in uncertainty that affect the stock equilibrium between liquid and illiquid assets.
The occurrence of a new-found belief firmly held, that a certain rate of inflation will occur, cannot affect the rate of interest. But the growth of uncertainty about what rate of inflation, if any, is in prospect, can send up the rate of interest. (Harrod 1971)Let us look in detail at each criticism.
- First, remember that there are three possible assets to choose from to hedge against inflation: money, bonds, and capital assets. At equilibrium, all three money-rates are equal and so no alternative is better than any other. Fisher’s theory assumes that r* is fixed for given time-preference and technology, and represents what people ultimately want—goods to consume. Of course, r* does not depend on the actual price of the asset because it is a required physical rate fixed by technology and tastes. However, the price of assets matters for the purchasing power—either directly by affecting the total return obtained after selling an asset or indirectly by affecting the creditworthiness of the asset owner. Thus, the arbitrage analysis should not start with real rate and go to nominal rate, but should start directly with nominal rates and compare cash outflows to cash inflows.
- Second, “so long as it is open to the individual to employ his wealth in hoarding or lending money, the alternative of purchasing actual capital assets cannot be rendered sufficiently attractive (especially to the man who does not manage the capital assets and knows very little about them), except by organizing markets wherein these assets can be easily realised for money” (Keynes 1936). Usually, capital assets are illiquid so that they cannot be resold at all or only by recording large capital losses. Thus, illiquid capital assets are “not […] a hedge against inflation and hence will be shunned by savers” (Davidson 1986, italics added). This, of course, goes against the more recent Monetarist development of Fisher’s theory that assumes that the relevant transmission mechanisms of a monetary shock goes beyond the portfolio adjustments in terms of financial assets to include also “such assets as durable and semi-durable consumer goods, structures, and other real property” like “houses, automobiles, […] furniture, household appliances, clothes, and so on” (Friedman 1974).
- The third and essential criticism of Fisher by Keynes is delivered in the following way:
There is no escape from the dilemma that, if it is not foreseen, there will be no effect on current affairs; whilst, if it is foreseen, the prices of existing goods will be forthwith so adjusted that the advantages of holding money and of holding goods are again equalized, and it will be too late for holders of money to gain or suffer a change in the rate of interest which will offset the prospective change during a period of the loan in the value of the money lent. For the dilemma is not successfully escaped by Professor Pigou’s expedient of supposing that the prospective change in the value of money is foreseen by one set of people but not foreseen by another. (Keynes 1936)
Thus, in any case, in the context of Fisher’s theory, the money holders (the lenders) will never be able to adjust the interest rate, i.e., the interest rate on bonds, before inflation occurs. After inflation occurred, money holders will not have any incentive to do any arbitrage because all money-rates will be equal again. In order to understand why, it is first necessary to understand how the rate of interest could go up because of perfectly expected inflation. This would not result from an arbitrage between money and bonds because both are monetary assets and so both are affected exactly in the same way by inflation:
Bonds and cash are two forms of asset denominated in money. Neither has a hedge against inflation. […] The rate of interest represents the rate at which bonds can be exchanged for cash. Since neither contains a hedge against inflation, the new-found expectation that inflation will occur cannot change their relative values or therefore, the rate of interest. […] The idea that new-found expectation can alter the relative value of two money-denominated assets, is logically impossible, and must not be accepted into the corpus of economic theory. (Harrod 1971)
The only reason why the interest rate would go up is because individuals want to switch their portfolio from monetary assets to liquid non-monetary assets. The problem is, then, to know if they actually can do this arbitrage based on perfectly expected inflation. Keynes’s answer is no. Indeed, on one side, if inflation was not foreseen (if neither borrowers nor lenders saw that a monetary shock occurred and so thought that i_0 = r*), then lenders did not have any incentive to raise the rate of interest and borrowers did not have any incentive to borrow. Once inflation occurred, those who are long in monetary assets record an unexpected loss in real terms (i_0 – π_2 < r*), whereas those who are long in capital assets record an unexpected gain in nominal terms (i_0 < r* + π_2); it is too late to make up for inflation—money holders record a loss that cannot be avoided by increasing i. At the same time, there is no more incentive for monetary-asset holders to do any more arbitrages because i_0 = r* again (assuming that no more inflation is expected).
(...)
3. THE TRANSFER OF REAL INCOME OVER TIME
Fisher assumes that the arbitrage that goes on at the microlevel between present and future income can be applied at the macroeconomic level with aggregate real income. This has, again, been criticized by Keynes (1936):
Actually, in his own terms, Fisher seems aware of this. He recognizes that a person can change his/her real income streams in two ways (Fisher 1930)—via their impatience (borrowing and lending) and via investment. However, at the aggregate level, the first solution is not possible:
Stated alternatively, the arbitrage process that leads to the condition of indifference cannot be applied at the aggregate level. Or, again, the loanable funds supply and demand functions do not exist at the aggregate level. He should have concluded that the market interest rate cannot be determined in this way, but he did do so and instead continued his analysis by assuming that all the results obtained from microeconomic reasoning apply at the macroeconomic level.
4. THE THEORY OF RATE OF INTEREST
Keynes (1937, 1936), Kregel (1988, 1999), and Kahn (1984) already made a criticism based on the same lines. Fisher assumes that r* is given by technology and tastes. r* is a physical rate of return. However, in his analysis, Fisher recognizes that r* is actually calculated in money terms and that price expectations matter for the decision—the rate of return over cost is the monetary expression of r* and is the essential variable for investment (Fisher 1930). Later, Keynes explicitly stated that the marginal efficiency of capital and the rate of return are identical concepts. One could then wonder if it is justified
to criticize Fisher’s analysis for not taking into account the importance of money and monetary expectations.
In fact, in Fisher’s theory, money is a veil and Keynes should not have confounded marginal efficiency of capital and marginal rate of return over cost as depicted by Fisher. Indeed, in Fisher, the real return is guaranteed because it depends on the technical capacity of the productive assets. Stated alternatively, the rate of return over cost is concerned with the “profit” obtained from the produced output expressed in monetary terms, whereas the marginal efficiency of capital is concerned with the profit obtained from the sale of the production. This should be clear if one reads the following quote:
Thus, the rate of return is just a monetary expression of the “primitive cost and return typified by labor and satisfaction” (Fisher 1930). On the other side, Keynes was very careful to state that the marginal efficiency of capital does not rest directly on technical concepts (Kregel 1988): “If capital becomes less scarce, the excess yield will diminish, without its having become less productive—at least in the physical sense” (Keynes 1936).
5. THE FISHER INDIFFERENCE CONDITION AS A DEFINITION
Some post-Keynesian authors, like Smithin (2003) or Cottrell (1994), even if they reject the notion of real rate of return, agree that the real rate of interest is a useful concept in terms of definition:
Second, the idea that Fisher’s real rate of interest is “just” a definition is not what Fisher had in mind. Fisher’s indifference condition reflects a hypothesis about the behavior of individuals and their method of selecting assets. It also reflects a particular conception of income (Kregel 1999). However, as shown above, this condition is problematic for several reasons. In addition, if one assumes that the real rate of interest is just a definition, one must assume that there is a clear correlation between inflation and nominal interest rates. However, as shown above, Fisher was the first to recognize that this is not the case. In fact, many studies, including Fisher, have shown that the “Fisher effect” does not hold.[주7] The following confirms the conclusion of Fisher. The analysis is divided in two parts. In the first part, the correlation between variables are checked and some conclusions are drawn. In the second part, a Granger causality test is performed to substantiate the previous conclusions.
Aggregate demand can be derived only from present consumption or from present provision for future consumption. The consumption for which we can profitably provide in advance cannot be pushed indefinitely into the future. We cannot, as a community, provide for future consumption by financial expedients but only by current physical output. In so far as our social and business organisation separates financial provision for the future from physical provision for the future so that efforts to secure the former do not necessarily carry the latter with them, financial prudence will be liable to diminishThus, not only is Fisher’s condition of indifference wrong at the microlevel, it is also wrong at the aggregate level.
aggregate demand and thus impair well-being, as there are many examples to testify. (Keynes 1936, italics added)
- In the former case, it does not automatically protect individuals against purchasing power loss, and
- in the second case, arbitrage is impossible because there are no spot and forward markets for a “commodity” called “aggregate income.”
Actually, in his own terms, Fisher seems aware of this. He recognizes that a person can change his/her real income streams in two ways (Fisher 1930)—via their impatience (borrowing and lending) and via investment. However, at the aggregate level, the first solution is not possible:
Borrowing and lending, the narrower method of modifying income streams, cannot be applied to society as a whole, since there is no one outside to trade with; and yet society does have opportunities radically to change the character of its income stream by changing the employment of its capital. (Fisher 1930)
Stated alternatively, the arbitrage process that leads to the condition of indifference cannot be applied at the aggregate level. Or, again, the loanable funds supply and demand functions do not exist at the aggregate level. He should have concluded that the market interest rate cannot be determined in this way, but he did do so and instead continued his analysis by assuming that all the results obtained from microeconomic reasoning apply at the macroeconomic level.
4. THE THEORY OF RATE OF INTEREST
Keynes (1937, 1936), Kregel (1988, 1999), and Kahn (1984) already made a criticism based on the same lines. Fisher assumes that r* is given by technology and tastes. r* is a physical rate of return. However, in his analysis, Fisher recognizes that r* is actually calculated in money terms and that price expectations matter for the decision—the rate of return over cost is the monetary expression of r* and is the essential variable for investment (Fisher 1930). Later, Keynes explicitly stated that the marginal efficiency of capital and the rate of return are identical concepts. One could then wonder if it is justified
to criticize Fisher’s analysis for not taking into account the importance of money and monetary expectations.
In fact, in Fisher’s theory, money is a veil and Keynes should not have confounded marginal efficiency of capital and marginal rate of return over cost as depicted by Fisher. Indeed, in Fisher, the real return is guaranteed because it depends on the technical capacity of the productive assets. Stated alternatively, the rate of return over cost is concerned with the “profit” obtained from the produced output expressed in monetary terms, whereas the marginal efficiency of capital is concerned with the profit obtained from the sale of the production. This should be clear if one reads the following quote:
In the real world our options are such that if present income is sacrificed for the sake of future income, the amount of future income secured thereby is greater than the present income sacrificed. […] Man can obtain from the forest or the farm more by waiting than by premature cutting trees or by exhausting the soil. […] Nature offers man may{many} opportunities for future abundance at trifling present cost. So also human technique and invention tend to produce big returns over cost. (Fisher 1930, italics added)
Thus, the rate of return is just a monetary expression of the “primitive cost and return typified by labor and satisfaction” (Fisher 1930). On the other side, Keynes was very careful to state that the marginal efficiency of capital does not rest directly on technical concepts (Kregel 1988): “If capital becomes less scarce, the excess yield will diminish, without its having become less productive—at least in the physical sense” (Keynes 1936).
5. THE FISHER INDIFFERENCE CONDITION AS A DEFINITION
Some post-Keynesian authors, like Smithin (2003) or Cottrell (1994), even if they reject the notion of real rate of return, agree that the real rate of interest is a useful concept in terms of definition:
Interest rates are determined in the financial sector proximately by the decision of the ultimate provider of credit, in other words the central bank. This institution also sets the pace for real interest rates, and not just for nominal rates. The real interest rate (on Fisher’s definition) is just the nominal rate minus expected inflation. Hence the central bank can set the real rate, if it wishes, simply by adjusting the setting of the nominal rate to offset changes in expectation of inflation (Smithin 2003).This position is, however, quite problematic for several reasons. First, it puts a real concept into the monetary framework. It is the relationship between nominal cash inflows and nominal cash outflows that matters, rather than the notion or “real” income. “Real” assumes that cash outflows are only linked to consumption and that the cash outflows of different economic agents are equally affected by inflation. It does not take into account the fact that the structure of spending, as well as financial commitments, are crucial for the effect of prices on cash-outflows. As Pigeon notes, for example, unionized workers in Canada have wage demands that “are anchored on expected inflation and interest rates” (Pigeon 2004). In itself, the real wage is an inefficient way to protect the purchasing power of wage; the whole range of cash outflows should be accounted for so as to protect the financial power of wage. It is the same with financial income earners whose consumption outflow is far less important in proportion than cash outflows due to financial commitments like interest, margin calls, or off-balance sheet commitments.
Second, the idea that Fisher’s real rate of interest is “just” a definition is not what Fisher had in mind. Fisher’s indifference condition reflects a hypothesis about the behavior of individuals and their method of selecting assets. It also reflects a particular conception of income (Kregel 1999). However, as shown above, this condition is problematic for several reasons. In addition, if one assumes that the real rate of interest is just a definition, one must assume that there is a clear correlation between inflation and nominal interest rates. However, as shown above, Fisher was the first to recognize that this is not the case. In fact, many studies, including Fisher, have shown that the “Fisher effect” does not hold.[주7] The following confirms the conclusion of Fisher. The analysis is divided in two parts. In the first part, the correlation between variables are checked and some conclusions are drawn. In the second part, a Granger causality test is performed to substantiate the previous conclusions.
5.1. Analysis of Correlations
(...)
(...)
, the 
![\begin{align}
&\text{Let }s = a + ar + ar^2 + ar^3 + \cdots + ar^{n-1}. \\[4pt]
&\text{Then }rs = ar + ar^2 + ar^3 + ar^4 + \cdots + ar^{n} \\[4pt]
&\text{Then }s - rs = s(1-r) = a-ar^{n},\text{ so }s = a \frac{1-r^{n}}{1-r}.
\end{align}](http://upload.wikimedia.org/wikipedia/en/math/a/b/4/ab40c376fc277aea250484fa64b8701c.png)
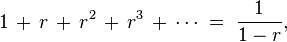
![\begin{align}
&\text{Let }s = 1 + r + r^2 + r^3 + \cdots. \\[4pt]
&\text{Then }rs = r + r^2 + r^3 + \cdots. \\[4pt]
&\text{Then }s - rs = 1,\text{ so }s(1 - r) = 1,\text{ and thus }s = \frac{1}{1-r}.
\end{align}](http://upload.wikimedia.org/wikipedia/en/math/c/a/e/caed3679cb96a5b26a3fcb30f2518e6d.png)
글
