자료 1: paran 사전 (원출처: 동서문화 PASCAL)
수열(數列) 
 ,
, 
 ,
, 
 , 이 있을때, 이것을 덧셈기호(+)로 연결한
, 이 있을때, 이것을 덧셈기호(+)로 연결한 
 +
+
 +…를 무한급수 또는 급수라 하며, 간단히
+…를 무한급수 또는 급수라 하며, 간단히  이라고 나타내기도 한다. 이것에서는 위와 같은수열을 순차적으로 배열하여 더하면 어떻게 되는가를 문제로 삼게 된다. 또 여기서,
이라고 나타내기도 한다. 이것에서는 위와 같은수열을 순차적으로 배열하여 더하면 어떻게 되는가를 문제로 삼게 된다. 또 여기서, 
 =
=
 +
+
 +
+
 +…+
+…+
 이라 나타내면 이것을 급수
이라 나타내면 이것을 급수 
 +
+
 +…의 제
+…의 제 부분합 또는 부분합이라 한다. (... 이하 생략 ...)
부분합 또는 부분합이라 한다. (... 이하 생략 ...)
자료 2: 수학사랑
무한수열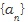 의 각 항을 차례로 합의 기호 + 로 연결한 식
의 각 항을 차례로 합의 기호 + 로 연결한 식 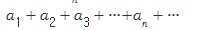 이 무한급수 또는 급수이다. (... ...)
이 무한급수 또는 급수이다. (... ...)
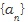 의 각 항을 차례로 합의 기호 + 로 연결한 식
의 각 항을 차례로 합의 기호 + 로 연결한 식 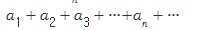 이 무한급수 또는 급수이다. (... ...)
이 무한급수 또는 급수이다. (... ...)
series를 왜 級數라고 번역했는지 그 이유를 알기는 어렵다.
일상적으로 級數는 '기술 따위의 우열에 따라 매기는 등급'을 의미한다.
그러나 수학에서의 級數에서는 그런 의미를 전혀 찾을 수 없다. series와 級數 사이에 다른 어떤 연관도 찾아보기 어렵기 때문에 級數는 series를 낱말 그대로 충실히 번역한 것으로 보기도 어렵다. 오히려 그 보다는 항이 순서 있게 무한히 엮여져 하나의 전체를 이루고 있는 그 형태를 적절히 나타내기 위해 series와 무관하게 만든 것으로 보인다.
일반적으로 무한급수 이 수렴하는지 또는 발산하는지 알기 위해서는 부분합의 수열 [, 즉]
이 수렴하는지 또는 발산하는지 알기 위해서는 부분합의 수열 [, 즉]
 이 수렴하는지 또는 발산하는지 알기 위해서는 부분합의 수열 [, 즉]
이 수렴하는지 또는 발산하는지 알기 위해서는 부분합의 수열 [, 즉]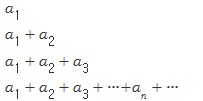
합의 수열을 고려하게 된다.
이때 각 항을 비교해 보면 '층계 또는 단계', 즉 級이 있다고 할 수 있다. 이러한 이유에서 級數라고 했을지 모른다.
자료 3: ...




댓글 없음:
댓글 쓰기